CMA考生需要通读教材,全面掌握CMA知识,然而教材知识过于复杂,无法阐明重点,所以需要重点总结,会计网为考生总结了预测技术中回归分析的知识点。

CMA重要知识点之预测技术—回归分析
回归分析用于预测两个或多个变量之间的直线关系,根据自变量的数量,可以分为单一回归变量分析(简单回归分析)和多元回归分析。
1、单一回归分析:Y=a+bX(一个自变量与一个因变量的抽样观测)
其中:Y=因变量;X=自变量;b=斜率(单位变动成本);a=常数(固定成本),注意口径及限定范围的问题
2、多元回归分析多个自变量与一个因变量的抽样观测相关系数
一般用字母r表示,用来衡量自变量(x)和因变量(y)之间线性关系的程度。r绝对值越接近1,两变量间线性相关程度越强。越接近于0,即|r|→0,则线性关系越弱,即变量之间的相关度低。
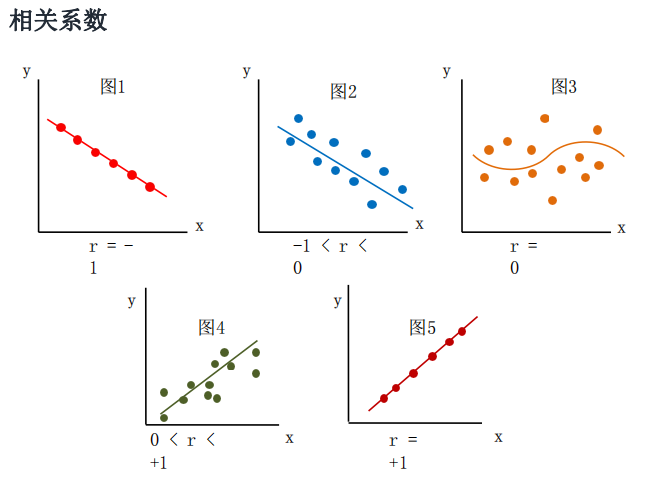
(1)r=-1→x和y之间为绝对负相关的线性关系,图1。
(2)-1<r<0→x和y之间为负相关的线性关系,图2。
(3)r=0→x和y之间没有线性关系,图3。
(4)0<r<+1→x和y之间为正相关的线性关系,图4。
(5)r=+1→x和y之间为绝对正相关的线性关系,图5。
回归分析的拟优合度
1、拟优合度R(R=r2)衡量因变量的变化可在多大程度上通过自变量的变化来解释;R取值介于0和1之间,数字越接近1,回归就越可靠。
2、R的现实意义是,如果R=0.9983,这表明有99.83%的因变量可以通过自变量来进行解释。
3、R值越大,公式的预测价值越高。
回归分析的优点
1、提高决策分析的客观性。
2、识别混合成本中的变动因素和固定因素。
3、帮助管理会计师预测,在成本动因发生变化之后,未来成本将如何变化。
回归分析的缺点
1、使用历史数据,当未来外部条件发生较大变化时,预测价值会下降。
2、假定变量之间存在着线性关系,但是这种假设并不完全成立。





















