Time Series中文名称为时间序列,它是ACCA考试MA科目中一个常考的重要考点之一,历年有很多考生都会在这个考点上失分,对此,会计网今天就为大家重点解析这个常考点内容,希望有所帮助。

01、Four components of a time series:
Trend -- underlying long-term movement over time in the values of the data recorded
趋势:数据的潜在变化情况
Seasonal variations – short-term fluctuations
季节性波动:短期数据波动
Cyclical variations – longer than seasonal variation
周期性变化:更长期的数据波动
Random variations – caused by unforeseen circumstances
随机事件
在MA中,通常只做短期预测,所以重点在于Trend 和Seasonal variation的掌握,不考虑Cyclical variations和Random variations.
02、Finding the Trend (T)
2.1 Moving average -- 移动平均法
移动平均法就是根据已知的实际数据,求出固定期数的平均值,且均值对应的时间点也是对应期数的中间点。我们来看一道例题:
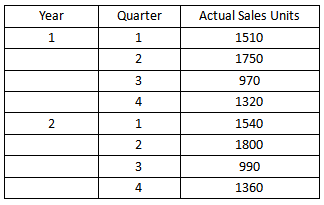
(1) Take a moving average over a period of three quarters.
第一种情况便是求奇数期数的移动平均数,所以第一个平均数=Year 1 Q1 - Q3实际销售数量的平均数,时间点对应的是Year1 Q2,第二个平均数=Year 1 Q2 - Q4实际销售数量的平均数,时间点对应的是Year1 Q3,以此类推,结果如图:
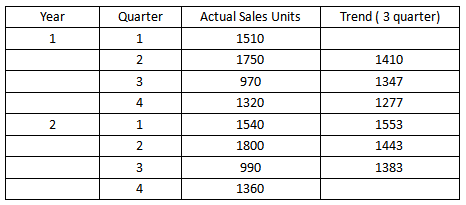
(2) Take a moving average over a period of four quarters.
第二种情况便是求偶数期数的移动平均数,第一个平均数=Year 1 Q1 - Q4实际销售数量的平均数,但是时间点对应的是Year1 Q2.5,第二个平均数=Year 1 Q2 - Year2 Q1实际销售数量的平均数,时间点对应的是Year1 Q3.5, 所以为了得到Q3对应的平均值,还需要再进行一次Q2.5和Q3.5的均值计算,结果如图:
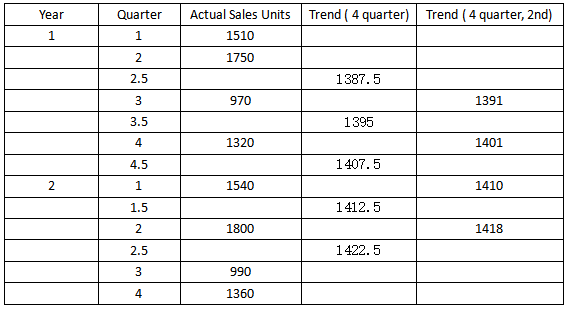
【总结1】:用移动平均法求奇数期的平均数时,只需求一次移动平均;求偶数期的平均数时,则需求两次移动平均
2.2 High-low method -- 高低点法
根据移动平均法求得的结果,我们可以提炼出来这样的数据:
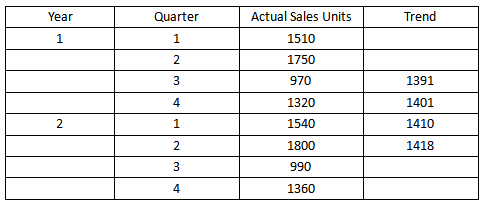
根据这些数据是可以利用线性回归法和高低点法求出Trend的表达式的,从而用于预测后面期数的Trend值。此时,以时间为自变量x,以trend值为因变量y。
当题中给了我们自变量的取值情况,按照题目要求进行计算。如果没有给出,默认Year1 Q1时x1=1, Year1 Q2时 x2=2 ...... 所以本题中高低点分别为:
Year1 Q3 x3=3, y3=1391
Year2 Q2 x6=6, y6=1418
带入高低点法公式:
![]()
Trend的最终表达式为 y = 1364 + 9x
【总结2】:移动平均法和高低点法是两种不同的方法,同学们要区分它们的适用情况
2.3 Deseasonalization/ seasonally-adjusted figure —— 去季节化
可以用两种模型:
(1) Additive model 加法模型 T=Y-S
(2) Multiplicative model 乘法模型 T=Y/S
(Y is the actual result in case)
【总结3】:看到Deseasonalization/ seasonally-adjusted figure的表达要知道是在让我们求出Trend的值,注意使用的是实际的Y
03、Finding the Seasonal Variation (S)
3.1 Additive model -- 加法模型
(1) S = Y – T
以上面数字为例
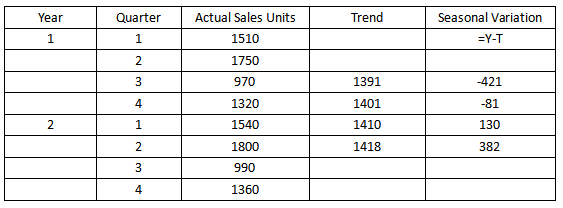
(2) 加法模型下季节性波动的总和为0,也就是
举例:当题目提供给我们第一年Q1对应的S1=+5,Q2对应的S2= -3,Q4对应的S4= -4,让我们求Q3的预计销量,那么此时就可以根据这个结论求出S3= 0 - (+5 -3 -4)= +2
(3) 对应期间的S是相等的
解释:当题目提供给我们第一年Q1对应的S1=+5,Q2对应的S2= -3,Q3对应的S3= +2,Q4对应的S4= -4,让我们求第二年Q2的预计销量,那么此时就可以直接将S2= -3代入计算
3.2 Multiplicative model -- 乘法模型
(1) S = Y /T
以上面数字为例
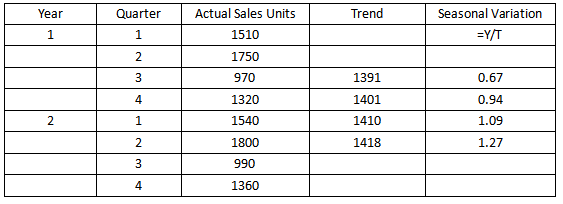
(2) 加法模型下季节性波动的总和为n,也就是
举例:当题目提供给我们第一年Q1对应的S1=1.1,Q2对应的S2= 0.8,Q4对应的S4= 1.4,让我们求Q3的预计销量,那么此时就可以根据这个结论求出S3= 4 - (1.1 + 0.8 + 1.4) = 0.7
(3) 对应期间的S是相等的
解释:当题目提供给我们第一年Q1对应的S1= 1.1,Q2对应的S2= 0.8,Q3对应的S3= 0.7,Q4对应的S4= 1.4,让我们求第二年Q2的预计销量,那么此时就可以直接将S2= 0.8代入计算
【总结4】:没有找到所求期间的季节性波动不要慌,仔细阅读一下题目看是否能够根据其他方式得到。
04、Finding the Forecast figure (Y)
4.1 Additive model -- 加法模型
Y = T + S
4.2 Multiplicative model -- 乘法模型
Y = T * S
两种方法下的T和S可以先根据之前介绍的方法确定,再带入公式进行计算就能得到最终的预测量了。所以同学们一定要注意审题,找到关键的提示信息,帮助我们解决问题。
以上就是时间序列相关的全部考点啦,同学们,你们学会了吗~
来源:ACCA学习帮